
There is an old-fashioned digital radio clock in our bedroom. Every time I wake up during the night, which happens a little too often at my age, the green glow of the digits is the first thing I see. Of course, the main intent is to see what time it is and whether I need to attempt to go back to sleep or I can call it a night. However, I also cannot avoid noticing if the time displayed is “interesting” in any way. By “interesting,” I mean, is it somehow distinctive? If it is, for some unknown reason, I sense a brief feeling of satisfaction. I believe, this is the secret of any aesthetic experience. It lies in our ability to discover a pattern in an observation. The more complex the pattern, the harder it is to discover, and greater in the aesthetic satisfaction.
So, what makes a particular time distinctive and, therefore, interesting? Let’s say the time is:
So, what makes a particular time distinctive and, therefore, interesting? Let’s say the time is:
This is clearly interesting because it is a specific full hour. There are only twelve of these out of the 720 (12 x 60) different time displays. But then there is just a single occurrence of say,
By that measure, this should be even more interesting. The reason it is not because there is no simple way to describe this number other than spelling out the whole number. Interestingness is connected with whether there is a shorter description that describes a class of objects other than complete enumeration. The 3’O clock time is a member of a class of times that can be described by the phrase “on the hour.”
However, when I look for interestingness in a clock display, I don’t just look at it as a time, but there are many different ways to look for patterns. Here are some examples:
Interesting as time: this is when the time itself is distinctive. Examples of this could be:
However, when I look for interestingness in a clock display, I don’t just look at it as a time, but there are many different ways to look for patterns. Here are some examples:
Interesting as time: this is when the time itself is distinctive. Examples of this could be:
Interesting as number: Here, the time is not important, but a sequence of integers may be distinctive. For example –
Mathematical relationships: There are cases where there is a more involved relationship between the digit sequence. For example, in the following example, each digit is double the previous digit:
Special Numbers: Sometimes, the number could be interesting because it has some special significance in nature. For example, the following example represents the first three digits of Pi in decimal –
Visually interesting: Sometimes, I see them not as numbers but as a geometrical pattern. In this example, one can see the vertical symmetry in the pattern of segments. That is, if we hold a mirror where the colons are, the two sides are mirror reflections of the other –
Secondary properties: There are times I would not see them as time, numbers, or visual patterns, but see it from the perspective of some other derived measure. For example, the two displays shown below have the quality that they have the largest numbers of segments that can be ON in a 12-hour clock display. They both have 20 segments that are ON, which is the maximum. Interestingly, if you measure the total light the clock casts in a dark room, these are the two times when the room would look the brightest, and it will be darkest at 1:11 –
What is most surprising is that a simple object like the display of a 4-digit clock has so many dimensions of interestingness. There are probably others, outside of the categories I listed above, that I have not discovered yet. Each of these dimensions represents a unique class of aesthetic experience. If you consider each class as a set, there are many individual members in each set. Therefore, the total number of time displays where one can derive aesthetic pleasure is surprisingly high. I will not be surprised if most of the 720 possible displays are interesting in one way or another. Let’s say we find some interesting property for 710 of these. Then the remaining 10 become distinctive because they don’t fall into any other category.
If a simple thing like a 4-digit clock display has so many aesthetic dimensions, imagine how many such dimensions may exist in most other complex objects like a flower, a sunrise, a person, or a relationship.
This is why I believe aesthetic exploration of anything in nature is essentially inexhaustible. One can always find yet another way to discover distinctness in any natural situation. No wonder we are still surprised by a sunrise or a love story. There is no fear of ever running out of artistic materials.
If a simple thing like a 4-digit clock display has so many aesthetic dimensions, imagine how many such dimensions may exist in most other complex objects like a flower, a sunrise, a person, or a relationship.
This is why I believe aesthetic exploration of anything in nature is essentially inexhaustible. One can always find yet another way to discover distinctness in any natural situation. No wonder we are still surprised by a sunrise or a love story. There is no fear of ever running out of artistic materials.
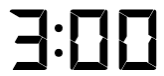
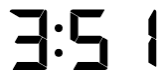
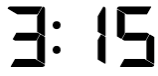
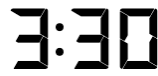
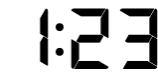

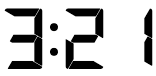
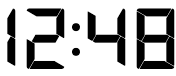
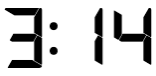
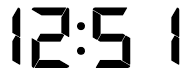
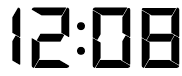
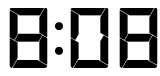
 RSS Feed
RSS Feed